Flexural Tests
The concrete strength used in the design of concrete pavements is based on AASHTO Test Method T-97 or ASTM C78, Flexural Strength of Concrete using a Simple Beam with Third-Point Loading (see Figure 1 below). These flexural tests (also called Modulus of Rupture tests or Third-Point Loading tests) are performed using concrete beams that have been cast and cured in the field, to mimic field conditions. For AASHTO thickness design, it is important that the third point loading 28-day flexural strength be used use in the AASHTO equation. If the strength values are measured using some other test method, it must be converted to the 28-day third-point strength.
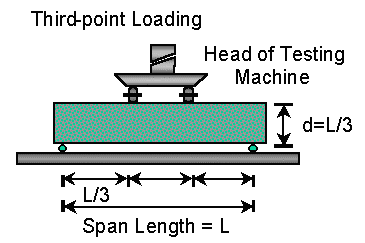
Figure 1. Third-Point Loading Flexural Strength Test
Some agencies use the center-point flexural strength test (AASHTO T-177 or ASTM C293) to determine their concrete strength (see Figure 2). Center-point loading forces the beam to fail directly under the center of the loading. This may or may not be the weakest point in the beam. In third point loading, the entire middle one-third of the beam is stressed uniformly and thus the beam fails at its weakest point in the middle one-third of the beam. By forcing the beam to fail at the center, the center-point flexural test results are somewhat higher than the third-point test results. Typically, the center point results are about 15% greater. Though this relationship is not exact, it does provide a reasonable estimate of the concrete's average strength.
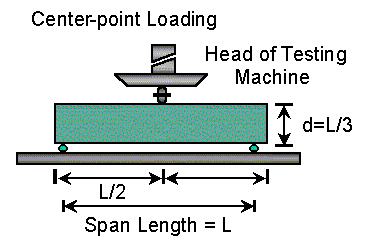
Figure 2. Center-Point Loading Flexural Strength Test
Compressive Tests
Many agencies use compressive strength of concrete cylinders or cores (AASHTO T-22 or ASTM C39) as an alternative to flexural strength testing (see Figure 3).

Figure 3. Photo of Compression Test
Splitting Tensile Tests
Splitting tensile tests involve compressing a cylinder or core on its side until a crack forms down the middle, causing failure of the specimen.

Figure 4. Diagram of Splitting Tensile Test
Correlation
There are many papers, articles, and opinions on the correlation between the different strength test types, and ACPA does not recommend any one test in particular. As for the correlation between the three test types, most of the following equations can be used, noting that the variance in the coefficients and equations can be attributed to regional, climatic, and material properties, among others.
Let:
Splitting Tensile Strength = Fst
Compressive Strength = Fc
Flexural Strength = MR (Modulus of Rupture), third-point loading (unless otherwise noted)
| Source/Author |
Equation in psi (pounds per square inch) |
| ACI Journal / Raphael, J.M. |
MR = 2.3 * [Fc ^(2/3)] |
| |
Fst = 1.7 * [Fc ^(2/3)] |
| ACI Code |
MR = 7.5 * [Fc ^(0.5)] |
| |
Fst = 6.7 * [Fc ^(0.5)] |
| Center for Transportation Research / Fowler, D.W. |
Fst = 0.72 x MR |
| Center for Transportation Research / Carrasquillo, R. |
MR (3rd Point) = 0.86 x MR (Center Point) |
| Greer |
MR = 21 + 1.254 Fst |
| |
MR = 1.296 Fst |
| |
MR = Fst + 150 |
| Hammit |
MR = 1.02 Fst + 210.5 |
| Narrow & Ulbrig |
MR = Fst + 250 |
| Grieb & Werner |
Fst = 5/8 MR (river gravel) |
| |
Fst = 2/3 MR (crushed limestone) |
NOTE: When High-Performance Concrete is used, the above relationhips will not necessarily hold true. The HPC mixes with very low w/c ratios tend to be more brittle and show different behaviors.
Additional Sources:
-
Raphael, J.M., "TENSILE STRENGTH OF CONCRETE," ACI Journal, Vol. 81, Number 2, Mar-Apr 1984 pp. 158-165
- Popovics, S., "Strength and related properties of concrete: a quantitative approach", New York, 1998.
- Grieb. W.E. and G. Werner, "Comparison of Splitting Tensile Strength of Concrete with Flexural and Compressive Strength," American Society for Testing and Materials, Proceedings, Vol 62, pp 972-995, 1962.
- Grieb, W.E., and Werner, G., “Comparison of the Splitting Tensile Strength of Concrete with Flexural and Compressive Strengths”, Public Roads, V. 32, No. 5, Dec. 1962, pp. 97-106.
The Importance of Using Average Strength
The expected actual average 28-day flexural strength (S'c) of the concrete should be used in thickness design procedures. Using the specified minimum construction strength will cause the design to be too conservative. Therefore, it is necessary to correct the specified minimum strength to the design strength using the following equation:
S'c = Sc + z(s)
where:
To use this equation, the designer must know or have estimate values of:
-
The percent of strength tests permitted below the specified level
-
The standard deviation of the strength tests.
The values for z are derived from basic statistics and are shown in the following table:
Values of the standard normal deviate (z) corresponding to the precent of tests below the specified strength (Sc) |
z |
Percent of specimens below the specified value |
.841 |
20 |
1.037 |
15 |
1.282 |
10 |
1.645 |
5 |
2.327 |
1 |
The standard deviation (s) of the strength test results depends upon the variability of the concrete and accuracy of the testing. Contractors generally use either central-mix or ready-mix plants to produce concrete. These plants are capable of providing very uniform concrete. Historically, the standard deviation (s) for ready-mix concrete is about 7 to 13 percent of the average strength. The standard deviation (s) for central-mix concrete is from 5 to 12 percent of the average strength. Generally, records of the standard deviation from past plant operations are available. The following example demonstrates the above procedure to account for the average, in-field 28-day flexural strength.
Example: Suppose that you want to design a small street project. You know that several local operators supply most of the concrete in your area using ready-mix concrete. You also know that you will specify concrete with a minimum 28-day flexural strength of 550 psi (3.79 MPa) and your specification will permit 10 percent of the tests to fall below that level. What strength do you use in the AASHTO design equation?
Step 1: Estimate the "s" using s = 9 percent of the flexural strength; or, call several ready mix operators to determine the value. Since you do not know the actual average strength, use the specified value for S'c (it will be fairly close). The value for s then becomes:
s = 0.09 (550)
s = 49.5 psi
Step 2: Estimate the design strength to use in the equation. Apply the correction for a 10 percent failure rate
(z: = 1.282)
S'c = 550+ 1.282(49.5)
S'c = 614 psi (4.22 MPa)
Note: The same principle applies if compressive strengths are used. The corrected compressive strength would be converted to third-point flexural strength using any one of the relationships previously shown. In the example, 614 psi (4.22 MPa) would be the value to use in the design equations. For comparison, the average 28-day flexural strength at the AASHO road test was 690 psi (4.76 MPa) third-point loading.


